The previous post described the methodology I’ve used to calculate similarities between recipes in cookit. If you haven’t read it I’ll give it 4 minutes because it will make understanding this post easier. Go one, I’ll wait.

It ended on a happy note and everything seemed to be downhill from there on. It was until I tried to run it. It took long. Very long. How long? I don’t know because I’ve canceled it after about one hour. Going with a famous quote (probably from Einstein, but there are some ambiguities in this subject)

Doing the same thing over and over again and expecting different results

I’ve decided to, once again, use math to assess how long the calculation will take.

Reminder - how similarities are calculated

In the previous post I’ve decided to calculate similarity by calculating the dot product between recipe ingredient vectors. In C# it will look more or less like this:

public float Similarity(Vector a, Vector b)
{
    float accumulator=0;
    for (int i = 0; i < a.Length; i++)
    {
        accumulator += b[i]*a[i];
    }
    var denom = Length(a)*Length(b); //convertion to absolute 
    return accumulator/denom;         //convertion to absolute    
}    

where Length looks like this:

public float Length(Vector a){    
    return (float)Math.Sqrt(a.Sum(value => value*value));
}

Complexity

To give you some scale. Cookit currently has:

• 182 184 recipes
• 2936 ingredients

As a consequence of the way I model similarities, I will need to create for each recipe a 2936 dimensional array representing ingredients. There are two things I should estimate: memory and number of calculations.
First the memory:

182184(number of recipes) * 2936 = 534 892 224 floats 
534 892 224 * 4(the size of float) ~ 2.14 Gig counting only space needed for floats

And if I will want to calculate the similarities for all recipes I will have to do:

((182184 * 2936)^2) /2 = 143 054 845 647 833 100 floating point multiplications

Is it much? Yes. Is it a lot for modern processors? IT Hare had a good article about the cost of each operation in the CPU. One note before we go further. Those calculations will be more for fun than actual time estimates. Even as IT Hate points out, trying to calculate the actual execution time in modern CPUs is hard enough to be pointless. But here we go:

143 054 845 647 833 100 * 5 (number of cycles for floating point operations) / 2 130 000 000 (this is what 2,13 GHz translates to - 2,13 billion operations per second)
This gives us ~ 335809496 seconds ~ 93280 hours ~ 3886 days  

Once again it is more for fun than anything else, but it appears that, citing Mark Watney

I will have to science the sh** out of it [youtube]

Assessing total time

To get a more real assessment how long will it take I’ve decided to do a test run on a small subset of recipes. Recipes are selected by selecting websites they are from, so my subset ended up being an unround 2199 recipes. Then I’ve made 3 test runs (I’ve learned the hard way that one test run doesn’t mean anything) and in average of 1530 seconds.

Now how to go from time of the subset to the time needed for all recipes? I can’t use it to assess the total execution time because it consists of two parts:

• calculating ingredient vector for all recipes.
• finding similar recipes for only 2199 one of them. The similarity is found by calculating one vector by all the others. So in this case I’ve done

182184*2199 = 400 622 616 vector multiplications

The first part is constant regardless how many similarities I will have to calculate.
The second part is directly proportional to the number of recipes for which I will calculate similarities.

The last missing piece for assessing the time of calculation for all recipes is the proportion of those two operations. So let’s fire up the profiler (dotTrace by choice) in sampling mode: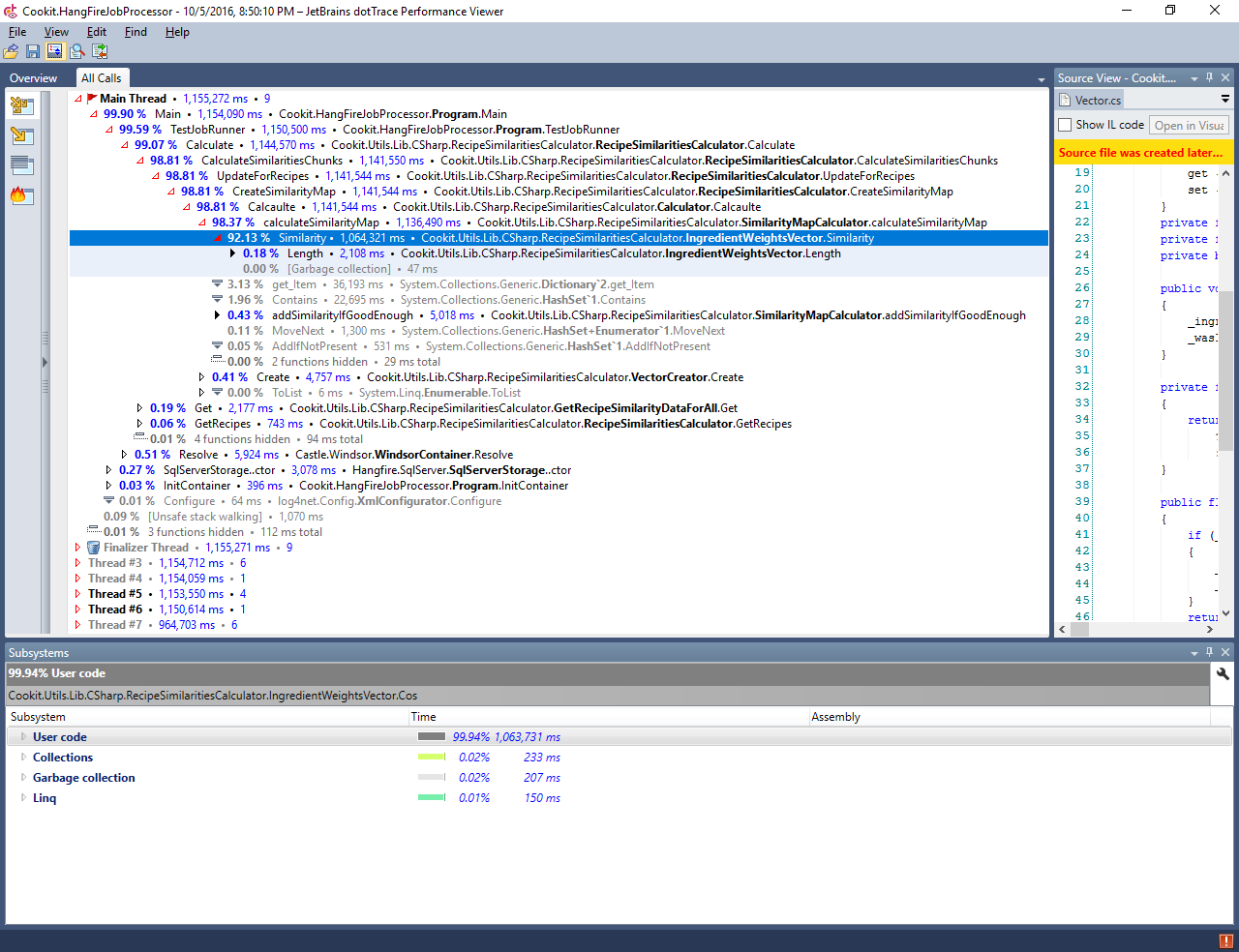

Well, bummer to put it lightly. Almost all time went into calculating the dot product (named here Similarity). From this I know that I can calculate the total time as a linear function from number of recipes without making to big of an error:

(1530 / 2199) * 182184 ~ 34 hours

where:
- 1530 - number of seconds it took
- 2199 - number of ingredients
- 182184 - number of recipes 

So the next step will be:

Optimising

Less means faster

The fastest code is the code that never runs

Following this mantra I removed the ingredients that are not used in any recipe.

This reduced the length of the vector to 1709 and the sample time be a whopping 562 seconds to 968 seconds. With some simple math:

(968 / 2199) * 182184 ~ 22,3 hours (starting from 34 hours)

This is a 34% improvement. Nice :)

So case closed? No. I believe I can do better. To have an idea let’s have a look with a profiler:

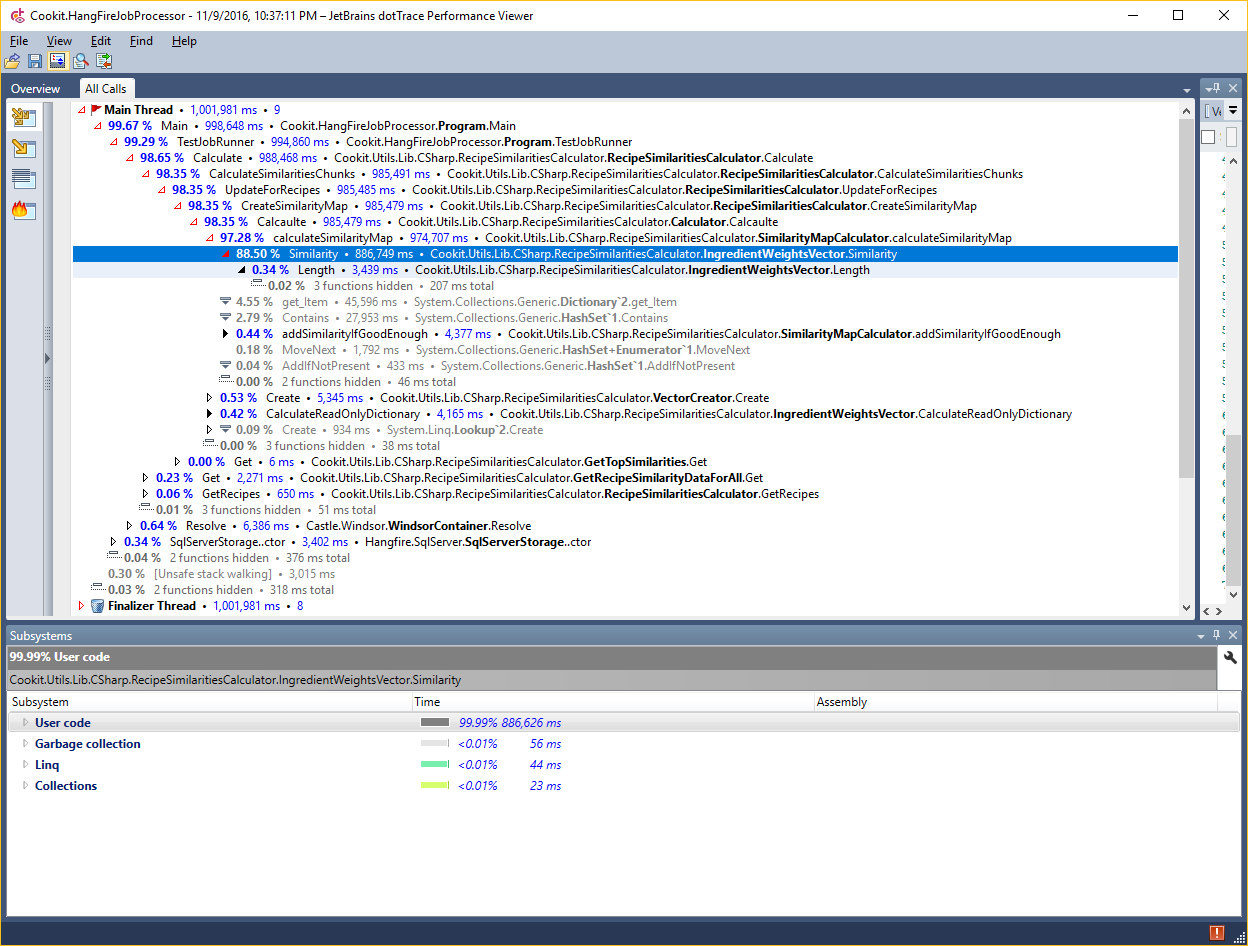
There did all the time go? Let’s have a look at another view:

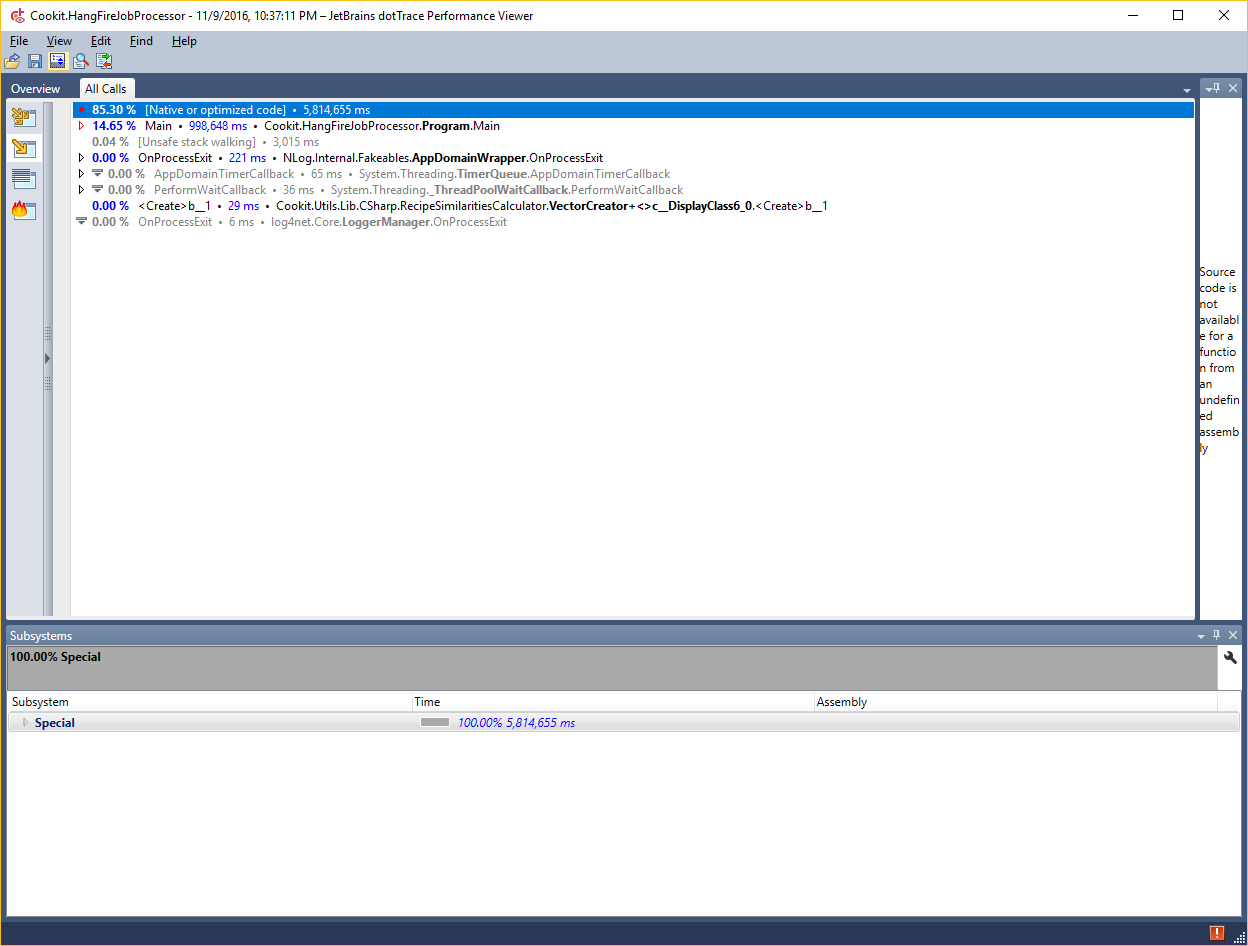
This shows that most of the time went into native code meaning in my case multiplying floats and iterating over the array. This means that this idea is a dead end. Let’s change the angle and use domain knowledge to optimize a bit more.

Using domain knowledge for optimization

I know that vectors are very sparse. In average one recipe has ~150 non-zero values in an almost 2.2k long array. This means I am wasting time multiplying zero. Let’s remove them.

Use a dictionary

Instead of using an array I will use a dictionary. The idea behind this take is this:

• it will allow me to store only those ingredients that the recipe has. This way the vector will shrink by an order of magnitude and as a side effect I will also shrink memory usage (although not that much since dictionary in .NET is a memory heavy structure)
• since I shrunk the vector I don’t need to enumerate over all the ingredients, but only over those from one of the vectors

So let’s put it into code:

public float Similarity(IDictionary<int,float> otherVector)
{
    var num = this
        .Sum(ingredient =>
        {
            float value = 0;
            if (otherVector.TryGetValue(ingredient.Key, out value))
                return ingredient.Value*value;
            return 0;
        });

    var denom = Length()*otherVector.Length();
    return num/denom;
}

With this change the calculation took 484 seconds. Scaling it to the full data set I get:

(484 / 2199) * 182184 ~ 11 hours (starting from 34 hours)

This means a 67% improvement over the starting value. So case closed? No. But this will be the topic for the next post since this one is getting to long.